Raymarching and Signed Distance Function (번역)

다음 글은 jamie-wong.com/2016/07/15/ray-marching-signed-distance-functions 블로그 글을 번역한 것입니다.

똥번역이어도 도움이 되었으면 좋겠습니다.

 

 

---

 

Signed Distance Functions

 줄여서 SDF. 특정한 공간상의 지점(point)의 좌표를 지정해주면 점과 어떠한 표면(surface)사이의 가장 가까운 거리를 반환하는 함수이다. 반환 되는 값의 부호(sign)는 그 점이 표면이 안쪽(inside)인지 바깥(outside)인지 를 나타낸다. (그래서 부호있는(signed) 거리(distance) 함수(function)이라는...)

 원점(origin)에 있는 구(sphere)를 고려해보자. 구 안쪽에 이는 점들은 원점으로 부터의 거리가 반지름(radius)보다 작을 것이고, 구 표면상에 있는 점들은 반지름과 거리가 동일할 것이며, 구의 바깥 쪽에 있는 점들은 반지름 보다 거리들이 크게 계산된다.

 우리의 첫번째 SDF, 즉 원점을 중점으로 하는 반지름이 1인 구는다음과 같다.

$f(x, y, z) = \sqrt{x^2 + y^2 + z^2} - 1$

 

다음 점들을 시도해보자.

 

$f(1, 0, 0) = 0$

$f(0,0,0.5) = -0.5$

$f(0,3,0) = 2$

 표면상의 점인 (1,0,0), 표면 안쪽이 있는 (0,0,0.5)은 표면과 가장 가까운 거리인 0.5 만큼 떨어져 있는 점이다. 그리고 (0,3,0)은 표면의 바깥에 있고 표면으로 부터 2만큼 떨어져 있는 점이다. 

 우리는 GLSL shader 코드로 작업할때, 공식은 다음과 같이 벡터화(vectorized: Raster그래픽스로 부터의 Vector 그래픽스의 생성)된다. Euclidean norm을 사용하여 아래와 같은 SDF를 쓸 수 있다.:

$f(\vec{p}) = ||\vec{p}|| - 1$

 

GLSL 로는 다음과 같이 작성가능하다.

float sphereSDF(vec3 p) {
    return length(p) - 1.0;
}

다른 편리하게 사용할 수 있는 SDF는 Modeling with Distance Functions 사이트를 참조하라.

 

---

The Raymarching Algorithm

 일단 우리는 몇몇의 모델링된 SDF를 알아보았다. 그렇다면 그것을 어떻게 렌더링하는가?

여기서 Raymarching Algorithm이 등장한다.

 Raytracing과 마찬가지로, 우리는 카메라 앞에 격자(grid)를 놓고 한 점을 선택한다. 그리고 격자 안의 각 점을 통해 카메라로부터 광선(ray)를 보내고, 각 격자점은 출력 이미지내의 픽셀에 대응된다.

 

From "Ray tracing" on Wikipedia

 차이점이라면 장면(scene)이 정의되는 방식에 있으며 그것들은 시야에 나온 광선(view ray)과 장면 사이의 교차점을 찾는 옵션에 따라 달라진다.

 

 Raytracing에서 장면은 일반적으로 명확한 기하학(geometry)적인 도형들(triangles, spheres 등등)으로 정의된다. 시야 광선(view ray)와 장면의 교점을 찾기 위해서 우리는 일련의 기하학적 교점(intersection) 판별(test)을 수행해야한다. (만약 교차한다면, 어디서 이 ray가 이 삼각형과 교차하는가? 이것은? 저것들은? 또한 저 구는? 등등과 같이...)

 

RayTracing의 튜토리얼을 원한다면 scratchapixel.com 를 참조해보자. 만약 당신이 한번도 ray tracing에 대해 보지 못했다면, 이 글의 나머지 부분이 약간 까다로울지도 모른다.

 

 Raymarching 에서 전체 장면은 signed distance function으로 정의된다. 시야 광선과 장면의 교차점을 찾기 위해서는 우리는 카메라로 부터 시작하여 시야 광선을 따라 점을 조금씩 이동한다. 각 단계에서 우리는 "이 점이 장면에 있는 표면 안쪽에 있는 점이야?" 라고 물어 볼 것이다. 다른 말로 하자면, "해당 점이 SDF로 값을 구해보니 음수(negative)값 이야?"가 될 것이다. 만약 그것이 그렇다면 우리는 된 것이다!. 우리는 무언가에 부딪힌 것이다. 만약 그렇지 않다면, 우리는 광선을 따라 최대(maximum)로 갈 수 있을때 까지 계속 진행한다.

 

From CPU Gems 2 : Chapter 8

 

 이 다이어그램에서 $\mathbf{p_0}$는 카메라다. 파란색 선은 카메라 $\rightarrow$ 뷰 평면(view plane)을 통과하는 광선의 방향과 같다. 첫번째 단계 ($\mathbf{p_0}$ $\rightarrow$ $\mathbf{p_1}$)는 꽤 크다(가장 가까운 표면으로부터의 거리만큼 이동한다). $\mathbf{p_0}$로부터 가장 가까운 점이 시야 광선을 따라 놓여 있지 않기 때문에 같은 방법으로 계속 이동 하다보면 우리는 결국 $\mathbf{p_4}$에 있는 표면에 도달하게 된다. 

 

GLSL로 구현해보면, 이 ray marching algorithm은 다음과 같다.

float depth = start;
for (int i=0; i<MAX_MARCHING_STEPS; ++i) {
    float dist = sceneSDF(eye + depth * viewRayDirection);
    if (dist < EPSILON) {
        //여기로 들어오면 우리는 scene의 표면 안쪽에 있는 것이다.
        return depth;
    }
    //뷰 광선을 따라 계속 움직인다.
    depth += dist;
    
    if (depth >= end) {
        //너무 멀리갔다. 포기
        return end;
    }
}

return end;

 

 위 코드에서 sceneSDF를 구 SDF로 하고, 뷰 광선 방향을 적절히 선택하기 위한 몇몇 코드를 더 작성해서 표면에 도달한 부분을 빨간색(red)로 마킹하면 우리는 다음과 같은 결과를 얻게 된다. 

 

 

자, 구(sphere)다! (아직 음영이 없다. 근데 구이긴 하다.)

 

 모든 예제 코드는  http://shadertoy.com/ 에 있다. Shadertoy는 OpenGL/WebGL 코드도 필요없이 shader 프로토타이핑을 가능하게 하는 도구이다. 당신은 vertex shader 코드를 작성할 필요가 없다. 당신은 단지 fragment shader 만 작성하면 된다.

 

 코드는 주석이 달려있고, 그래서 당신은 해당 코드들을 확인할 수 있으며 몇몇가지 실험을 해볼 수 있다. shader 코드의 각 파트의 상단에 우리는 당신의 이해를 돕기위해 테스트 해볼 수 있는 몇 개의 도전과제들을 남겨두었다. 코드를 보려면 위 이미지에 마우스를 올리면 나타나는 제목(Ray Marching: Part 1)을 클릭해봐라.

 

 

---

 

Surface Normals and Lighting

 컴퓨터 그래픽스에서 대부분의 라이팅 모델들은 surface normals 이라는 개념을 사용하여 표면상의 주어진 점에 대한 재질의 색상을 계산한다. 표면들이 명확한 기하도형(폴리곤 같은)에 의해 정의될 때, 법선(normals)들은 각각의 정점(vertex)에 지정되며 면(face)의 법선은 해당 면을 만들기 위한 정점에 지정된 법선의 보간(interpolating)에 의해 알아낼 수 있다.

 

 그렇다면 이제 우리는 어떻게 SDF에 의해 정의된 장면을 위한 표면 법선을 알아낼 것인가? 우리는 기울기(gradient : 벡터미적분학에서 스칼라장의 최대증가율(differential)을 나타내는 벡터장. 일단은 최대기울기를 나타낸다고 이해했음)를 사용할 것이다! 개념적으로, 함수 $f$에 대해 주어진 점(point) $(x, y, z)$ 의 gradient는 $(x, y, z)$위치에서 가장 빠르게 증가하는 $f$ 값의 방향을 알려준다. 이것은 우리의 surface normal이 될 것이다. (역주: 아직 무슨 말인지 못알아 먹겠음. 왜 빠르게 증가하는게 surface normal인지?)

 

 직관적으로, 표면상의 한 점에 대한 $f$ (우리의 SDF)값은 0으로 계산(evaluates)된다. 표면 안쪽(inside)에 있는 점에 대한 $f$값은 음수(negative)고, 바깥쪽(outside)의 값은 양수(positive)이다. 그렇기 때문에 음수에서 양수로 값이 변할때 가장 빠르게 $f$값이 변하며 그 방향이 표면과 직교(orthogonal, 문맥상 표면에 수직이라는 뜻)한다는 것을 알 수 있다. (이제 알아 먹겠음. ^^/)  

 

  $f (x, y, z)$의 gradient 는 $\nabla{f}$로 표현한다. 그리고 이것을 다음과 같이 계산할 수 있다.

$\nabla{f} = \left(\frac{\partial{f}}{\partial{x}},\frac{\partial{f}}{\partial{y}},\frac{\partial{f}}{\partial{z}}\right)$ 

 

 여기서 편미분 계산을 할 필요는 없다. 함수의 실제 도함수(real derivative)를 사용하지는 않고, 대신 우리는 표면상의 해당 점 주변의 점들을 샘플링(sampling)하는 것으로써 그것(미분값)의 근사(approximation)를 계산할 것이다. 그것은 당신이 미분을 배우기전에 rise-over-run으로 함수의 기울기를 계산하는 법을 배우는 것과 꽤 유사하다. (rise : y의 증감, run : x 의 증감, 즉 $\frac{f(x_2) - f(x_1)}{x_2 - x_1}$)

 

rise-over-run method from https://gaussian37.github.io/math-mfml-basic_calculus

 

$\vec{n} = \left[ \begin{array}{c} f(x + \varepsilon, y, z) - f(x - \varepsilon, y, z) \\ f(x, y + \varepsilon, z) - f(x, y - \varepsilon, z) \\ f(x, y, z + \varepsilon) - f(x, y, z - \varepsilon) \end{array} \right]$

 

/**
 * SDF의 gradient를 사용하여 표면상의 지정된 점 p의 법선(normal)을 추정한다
 */
vec3 estimateNormal(vec3 p) {
    return normalize(vec3(
          sceneSDF(vec3(p.x + EPSILON, p.y, p.z))
        - sceneSDF(vec3(p.x - EPSILON, p.y, p.z)),
          sceneSDF(vec3(p.x, p.y + EPSILON, p.z))
        - sceneSDF(vec3(p.x, p.y - EPSILON, p.z)),
          sceneSDF(vec3(p.x, p.y, p.z + EPSILON))
        - sceneSDF(vec3(p.x, p.y, p.z - EPSILON))
    ));
}

 

 이 지식으로 무장한다면, 우리는 표면상의 어떠한 지점에 있는 법선도 계산할 수 있다. 그리고 두 개의 광원(light)을 사용하여 Phong reflection model 이 적용된 다음과 같은 결과를 얻었다.

 

 

 기본적으로 이 포스트에서 모든 쉐이더(shaders) 애니메이션들은 전부 당신의 컴퓨터가 제트기 이륙하는 소리를 내는 것을 방지하기 위해 정지되어 있는 상태이다. (노트북 팬 돌아가는 것을 의미하는듯) 위 shadertoy 결과물에 마우스를 올려놓고 play 버튼을 누르면 애니메이션 이펙트를 볼 수 있다.

 

 

---

 

 

Moving the Camera

 나는 이것에 연연하지 않을 것이다. 왜냐하면 이 해결책은 ray marching 의 고유한 방법이 아니기 때문이다. raytracing 과 같이, 카메라를 변환(transformation)을 하기 위해 뷰 광선을 변환 행렬(matrix)들을 통해 이동/회전 하면 된다. 무슨 말인지 모르겠다면 scratchapixel.com 에 있는 ray tracing 튜토리얼을 참고하라. 또는 이 codinglabs.net 을 참고해도 좋다.

 

 일련의 평행이동(translations)과 회전(rotations)에 기반하여 카메라의 방향이 결정되는 방법을 알아내는것이 항상 직관적이지는 않다. 더 좋은 방법은 "나는 이 지점에 있는 카메라에서 저 지점을 바라보는 카메라를 원해!" 라고 생각해 보는 것이다. 이것은 정확히 OpenGL의 gluLookAt 함수가 해준다. 

 

 쉐이더더 내에서 우리는 해당 함수를 사용할 수 없다. 그러나 man gluLookAt 을 실행하여 man page 를 볼 수있고 어떻게 변환 행렬을 계산하는지 알아 낼 수 있다. 그리고 GLSL로 만들어본다면~

 

/* 주어진 eye point, camera target, up vector로 만들어진 view space상의
 * ray를 world좌표계로 변환하는 행렬을 리턴한다.
 *
 * 이것은 ray marching 방향을 계산할때 카메라의 중심이 view space상의 음의z축에
 * 정렬되어 있다고 가정한다.
 */
mat4 viewMatrix(vec3 eye, vec3 center, vec3 up) {
    vec3 f = normalize(center - eye);
    vec3 s = normalize(cross(f, up));
    vec3 u = cross(s, f);
    return mat4(
        vec4(s, 0.0),
        vec4(u, 0.0),
        vec4(-f, 0.0),
        vec4(0.0, 0.0, 0.0, 1)
    );
}

 

모든 구는 모든 각도에서 같게 보이기 때문에, 나는 여기서 cube 로 변경하겠다. 카메라는 (8, 5, 7)에 놓여있고 원점을 바라보도록 우리의 새로운 viewMatrix 함수를 이용하여 계산하였다. 그래서 우리는 다음과 같은 결과를 얻었다.

 

 

 

---

 

 

Constructive Solid Geometry

Constructive solid geometry(CSG)는 간단한 boolean 연산을 수행하여 복잡한 기하도형을 만드는 방법이다. Wikipedia의 이 그림은 이 기술로 어떤것이 가능한지 보여준다

 

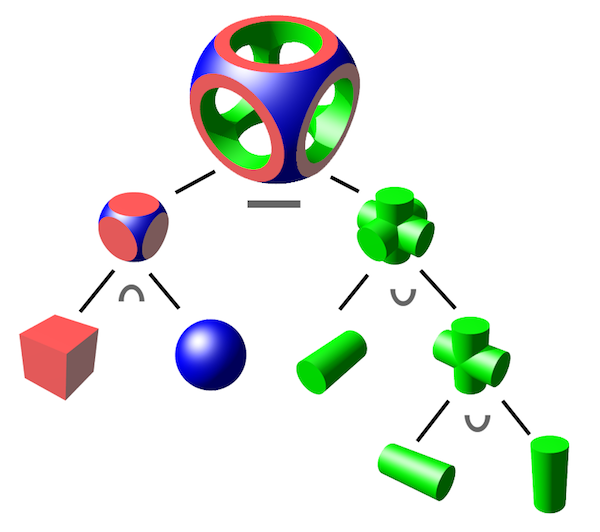
From "Constructive solid Geometry" on Wikipedia

 

 CSG 는 3개의 기본(primitive) 연산(operation)으로 이루어져 있다. : 교집합(intersection)(∩), 합집합(union)(∪), 차집합(difference)(-)

 

이러한 연산들은 SDF로 표현된 두 개의 표면들에 대한 결합을 모두 간결하게 표현 할 수 있다.

float intersectSDF(float distA, float distB) {
    return max(distA, distB);
}

float unionSDF(float distA, float distB) {
    return min(distA, distB);
}

float differenceSDF(float distA, float distB) {
    return max(distA, -distB);
}

 만약 다음과 같은 장면을 셋팅한다면:

float sceneSDF(vec3 samplePoint) {
    float sphereDist = sphereSDF(samplePoint / 1.2) * 1.2;
    float cubeDist = cubeSDF(samplePoint) * 1.2;
    return intersectSDF(cubeDist, sphereDist);
}

  다음과 같은 결과를 얻는다. (1.2 로 나누고 곱하는 것은 하단의 Uniform scaling 문단에서 설명할 것이니 지금은 넘어가자)

 

 

 이 Shadertory 의 코드를 편집해서 union 과 difference 연산을 실험해 볼 수 있다.

 

 이항연산으로 SDF의 의해 생성된 결과가 왜 그렇게 작동하는지에 대해 직관을 구축해 보는 것은 흥미롭다. 

$\begin{align}sceneSDF(\vec{p}) &= intersectSDF(cube(\vec{p}), sphere(\vec{p}))\\&= max(cube(\vec{p}), sphere(\vec{p}))\end{align}$

 

 

 SDF는 표면의 내부영역이 음수로 표현된다는 것을 기억해보자. 위 교집합 연산에서 만약 $cube(\vec{p})$와 $sphere(\vec{p})$가 둘 다 음수라면 $sceneSDF$는 음수만 될 수 있을 것이다. 이것은 한 지점이 cube 와 sphere 내부에 있는 지점이어야만 내부에 있다는 것을 의미한다. 이 결과는 정확히 CSG의 교집합 연산의 정의와 일치한다!

 

 같은 로직(logic)을 합집합 연산에 적용해봐도 동일하다. 만약 함수가 둘 다 음수라면, sceneSDF의 결과는 음수일테고, 표면 내부일 것이다.

$\begin{align}sceneSDF(\vec{p}) &= unionSDF(cube(\vec{p}), sphere(\vec{p}))\\&= min(cube(\vec{p}), sphere(\vec{p}))\end{align}$

 

 차집합 연산은 가장 까다롭다.

$\begin{align}sceneSDF(\vec{p}) &= differenceSDF(cube(\vec{p}), sphere(\vec{p}))\\&= max(cube(\vec{p}), -sphere(\vec{p}))\end{align}$

 

 SDF의 음수가 의미하는게 무엇일까?

 

 SDF의 양수와 음수값의 의미를 다시한번 생각해본다면, SDF의 음수라는 것은 표면의 내부와 외부가 반전이 된다는 것을 의미한다. sphere 의 내부 영역은 이제 모두 외부영역으로 고려될 것이고 그 반대도(외부영역은 내부영역으로 고려됨) 마찬가지이다.

 

 이것은 차집합이 첫번째 SDF와 두번째 SDF의 역(inversion)의 교집합이라는 것을 의미한다. 그래서 첫번째 SDF가 음수이고 두번째 SDF가 양수일때 음수값이 나온다. (역주: 왜 계속 음수값이 나온다는 것을 강조하냐면 SDF값이 음수가 되어야 표면의 내부영역이고 ray marching 알고리즘에서 sceneSDF 의 값이 음수값 - 즉, 내부영역에 도달해야만 이동하는 것을 멈추고 표면에 닿았다고 판단 하기 때문이다)

 

  기하학적인 용어로 전환해보면, 첫번째 표면의 내부와 두번째 표면의 외부에 있을때 장면 표면의 내부에 있다는 것을 의미하고 이것은 CSG 차집합 연산의 정의와 정확히 일치한다! 

 

 

---

 

 

Model Transformations

 카메라가 움직일 수 있다는 것은 약간의 유연함을 주지만, 장면의 일부분이 제각각 움직일 수 있다는 것은 확실히 더 많은 것을 제공한다. 어떻게 그것을 하는지 탐험해보자. 

 

Rotation and Translation

 SDF로 모델링된 장면을 평행이동하거나 회전하기 위해서는, SDF로 계산하기 전에 각 점에 역변환(inverse transformation)을 적용 해야 한다.

 

 다양한 변환들을 다양한 메쉬들에게 적용할 수 있는 것 처럼, 다양한 변환들을 SDF의 각 부분에 적용 할 수 있다. 그냥 원하는 SDF의 각 부분에 변환된(transformed) ray를 보내기만하면 된다. 예를들어 sphere는 그대로 두고, 여전히 교집합된 상태로 cube 를 상하로 흔들려면 다음과 같이 하면 된다. :

 

float sceneSDF(vec3 samplePoint) {
    float sphereDist = sphereSDF(samplePoint / 1.2) * 1.2;
    float cubeDist = cubeSDF(samplePoint + vec3(0.0, sin(iGlobalTime), 0.0));
    return intersectSDF(cubeDist, sphereDist);
}

 Shadertoy 참조 노트 : iGlobalTime 은 Shadertoy에서 셋팅한 uniform 변수인데, 플레이를 시작했을 때부터 흐른 시간(seconds)이다.

 

 

위와 같은 변환을 수행했다면 이것은 여전히 signed distance field 의 결과일까? 회전과 평행이동의 경우, "강제(rigid body) 변환"이기 때문에 점들간의 거리가 보존된다는 것을 의미한다.

 

일반적으로 당신은 변환행렬(transformation matrix)의 역행렬을 샘플링된 점(역주: 일반적으로는 vertex들이 될 것이다0에 곱함으로써 여러 강체 변환을 적용 할 수 있다.

 

 예를들어 만약 회전 행렬을 적용하고 싶다면 다음과 같이 하면된다 :

mat4 rotateY(float theta) {
    float c = cos(theta);
    float s = sin(theta);
    
    return mat4(
        vec4(c, 0, s, 0),
        vec4(0, 1, 0, 0),
        vec4(-s, 0, c, 0),
        vec4(0, 0, 0, 1)
    );
}

float sceneSDF(vec3 samplePoint) {
    float sphereDist = sphereSDF(samplePoint / 1.2) * 1.2;
    vec3 cubePoint = (invert(rotateY(iGlobalTime)) * vec4(samplePoint, 1.0)).xyz;
    float cubeDist = cubeSDF(cubePoint);
    return intersectSDF(cubeDist, sphereDist);
}

 

... 하지만 여기서 당신이 WebGL을 사용하고 있다면, GLSL안의 inversion matrix 와 같은 builtin 함수가 없다. 하지만 반대(opposite)의 변환을 수행할 수 있다. 위의 scene function은 다음과 동일하게 변경할 수 있다. :

float sceneSDF(vec3 samplePoint) {
    float sphereDist = sphereSDF(samplePoint / 1.2) * 1.2;
    vec3 cubePoint = (rotateY(-iGlobalTime) * vec4(samplePoint, 1.0)).xyz;
    float cubeDist = cubeSDF(cubePoint);
    return intersectSDF(cubeDist, sphereDist);
}

 

 더 많은 변환행렬들은 다른 그래픽스 교재를 참고하거나 다음 slide를 체크해보자. 3D Affine transforms.

 

 

Unniform Scaling

 좋다! 이제 위에서 얼버무렸던 이 이상한 스케일링 트릭으로 돌아가보자. (1.2 곱하고 나누는것):

float sphereDist = sphereSDF(samplePoint / 1.2) * 1.2;

1.2로 나누는 것은 sphere를 1.2배 확대하는 것이다.(우리가 특정 점(samplePoint)에 대해 SDF계산 하기 전, 역변환을 적용한다는 것을 기억해보자. 역주: 역변환이므로 1.2를 나누는것이 확대 하는 것임) 하지만 그 뒤에 왜 스케일링 팩터를 다시 곱할까? 단순하게 생각하기 위해 1.2 대신 2라고 생각해보자.

float sphereDist = sphereSDF(samplePoint / 2) * 2;

  스케일링은 강체 변환이 아니다. - 그것은 점들간의 거리가 보존되지 않는다. 만약 (0, 0, 1)과 (0, 0, 2)를 2로 나누어 변환한다면 (모델의 uniform upscaling이다), 점들간의 거리는 1에서 0.5로 변한다.

 

$\begin{align} ||(0, 0, 1) - (0, 0, 2)|| &= 1 \\ ||(0, 0, 0.5) - (0, 0, 1)|| & = 0.5 \end{align}$

(역주 : 원문에서는 두번째 수식이 ||(0, 0, 1) - (0, 0, 0.5)|| = 0.5 로 표현되어 있는데, 2로 나누었다는 표현에 맞게 순서를 뒤집었다.)

 

 그래서 우리가 sphereSDF에서 거리가 변화된 점들을 계산할 때, 그 점들에 대해서 우리는 실제 변환된 sphere의 표면으로 부터의 거리의 반(half)을 구하게 된다. 최종단계에서의 곱은 이러한 왜곡을 상쇄시킨다.

 

 흥미롭게도 만약 쉐이더에서 scale 보정을 하지 않거나 scale 보정값보다 더 작은 값을 사용하거나 해도 정확히 같은 결과로 렌더링된다! 

 왜 그런걸까??

 

//아래의 모든 것들은 모두 같은 결과의 이미지를 렌더링한다.
float sphereDist = sphereSDF(samplePoint / 2) * 2;
float sphereDist = sphereSDF(samplePoint / 2);
float sphereDist = sphereSDF(samplePoint / 2) * 0.5;

 SDF를 어떤 식으로 확대를 해도 거리의 부호(sign)값은 여전히 같다는 것을 주목해보자. "signed distance field"의 부호(sign) 부분은 여전히 같지만, 거리(distance) 부분은 이제 틀린 값인 것이다. 

 

 이 문제가 왜 그런지 보기 위해 우리는 ray marching algorithm 이 어떻게 작동하는지를 다시 한번 살펴볼 필요가 있다.

 ray marching algorithm 의 모든 단계에서 표면으로 부터의 가장 가까운 거리만큼 view ray의 방향을 따라 이동하게 된다. 표면으로 부터 가장 가까운 거리를 구하기 위해 우리는 SDF를 사용한다. 알고리즘을 빠르게 수행하기 위해서, 이 거리값이 가능한 큰 값이 되기를 기대하지만 만약 우리가 그 보다 작은 값(undershoot)(역주: 표면으로 부터의 가장 가까운 거리보다 작은 값)을 사용한다고 하더라도 여전히 알고리즘은 동작한다. 단지 더 많은 반복된 단계를 거칠 뿐이다.

 

 그리나 각 단계의 이동 거리에 SDF값보다 더 큰 값(overstimate)을 사용하는 것은 문제가 된다. 만약 다음과 같이 모델의 크기를 축소하려고 할때 축소 보정 값을 곱하지 않는다면 :

float sphereDist = sphereSDF(samplePoint / 0.5);

이제 구(sphere)는 완전히 안보이게 된다. 우리가 SDF에서 반환한 거리보다 큰 값을 사용한다면 raymarching algorithm은 아마 표면을 지나치게 될것이고 다시는 표면을 찾지 못하게 된다.

 

 그래서 우리는 안전한 uniform scale을 수행하기 위해 다음과 같이 한다 :

float dist = someSDF(samplePoint / scalingFactor) * scalingFactor;

 

 

Non-uniform scaling ans beyond

 모델을 균일하게 스케일링하길 원한다면 위에 섹션에서 언급된 distance overstimation 문제를 피하려면 어떻게 해야할까? uniform scaling과는 다르게 변환에 의해 발생한 거리 왜곡을 정확히 보정할 수 없다. uniform scaling 에서만 보정이 가능한 이유는 모든 차원들이 같게 확대/축소 되었기 때문에 표면상에서 sampling된 지점과 가장 가까운 점이 어디에 있든 scaling 보정(compensation)은 같다.

 

 그러나 non-uniform scaling에서는 거리에 의해 얼마나 많은 보정(correct)을 해야 할지 알기 위해 표면상의 가장 가까운 점을 알 필요가 있다.

 

 이 상황이 왜그런지 보기위해 다른 차원들(y,z)는 보존되지만 x-축(x-axis)에 대해 크기가 반으로 축소된 단위구(unit sphere)의 SDF를 고려해보자. 

$sphereSDF(x, y, z) = \sqrt{(2x)^2 + y^2 + z^2} - 1$

 

 만약 (0, 2, 0)에서 SDF를 계산한다면 1unit 의 거리를 얻을 것이다. 이것은 올바르다: 구의 표면에서 가장 가까운 점은 (0, 1, 0)이다. 하지만 만약 (2, 0, 0)을 계산한다면, 3unit의 거리를 얻을 것이다. 이것은 틀린 값이다. 표면상에서 가장 가까운 점은 (0.5, 0, 0)이다. 월드좌표계(world-coordinate)상의 거리는 1.5unit 이다.

 

 그래서 uniform scaling과 같이 거리를 넘어가는 것(overstimating)을 피하기 위해 SDF에 의해 반환되는 거리를 보정할 필요가 있다. 하지만 어떻게 할까? 과도한 보정치(overstimation factor)는 표면이 어디에 있는가와 어느 점인지에 따라 달라진다.

 

 보통은 부족한 거리가 용납되기 때문에(역주 : 위 raymarching algorithm 설명에서 marching distance가 작은것은 성능에 문제가 있는 것이지 결과에 영향을 미치지는 않기 때문인듯) 다음과 같이 가장 작은 scaling factor를 곱하면 된다. :

float dist = someSDF(samplePoint / vec3(s_x, s_y, s_z)) * min(s_x, min(s_y, s_z));

 다른 비강체(non-rigid)변환들도 원리는 같다.: 변환에 의해 부호(sign)가 보존되는 한, 표면까지의 거리를 절대 넘지않는(overstimating)  약간의 보정(compensation factor)치만 필요하다는 것을 알게될 것이다.

 

 

---

Putting it all together

이 포스트에서 기본적인 도구들로 당신은 몇몇의 이쁘고 흥미로운 것들을 만들어서 복잡한 장면을 만들 수 있다. ambient/diffuse와 같은 재질의 요소를 일반적인 벡터(vector)를 사용한 간단한 트릭을 조합하고, 이 포스트의 시작부분의 몇개의 쉐이더를 생성할 수 있다. :

 

 

 

---

 

Reference

 signed distance function들에 대해 더 많은 배움의 길이 있다. 이 주제에 있어 가장 왕성한 저자중의 한 명은 Inigo Quilez이다. 나는 이 포스트의 대부분의 컨텐츠를 그의 shader code와 웹사이트를 읽음으로써 배웠다. 그는 또한 Shadertoy의 공동개발자의 한 명이다.

 그의 사이트에 흥미로운 SDF관련된 자료들 중에는 내가 다루지 않은 smooth blending between surface 와 soft shadow가 있다. 

 

다른 참고자료

• GPU Gems 2 : Chapter 8. Per-Pixel Displacement Mapping with Distance Funtions
• Raymarching Sample Code on Shadertoy
• Modeling with Distance Functions